フーリエ変換、窓関数
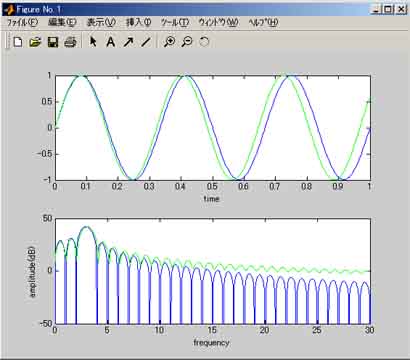
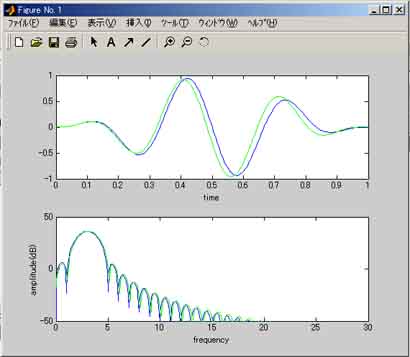
さて、いきなり周波数分析と言われても、信号処理を知らない人には
何の事かわからないでしょう。
普通、一般的にSIN波やCOS波などの波形を書く時の横軸は「時間」です。
これが、一般的ですよね。
そこで、フーリエ変換をする事により、横軸が「周波数」となるわけです。
一般的にフーリエ変換して求めた波形をスペクトルと言います。
縦軸に振幅を示した場合は振幅スペクトル、位相の場合は位相スペクトルと言います。
こういった、横軸を周波数として分析して行く事を周波数分析と言います。
さて、フーリエ変換をする場合は、原則として窓関数というものをかけます。
窓関数というのは、代表的な物に、以下のような関数があります。
・方形窓＝図紫色
・ハミング窓＝図青色
・ハニング窓＝図緑色
・ブラックマン窓＝図赤色
とあります。具体的には、下のような波形になります。
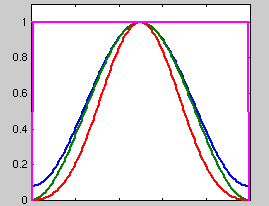
窓関数というのは、取り出されたデータに対して、重みをつける関数です。
方形窓は全てに対して一様な重みですが、他のものは中央部に重みがかかります。
さて、なぜ窓関数が必要なのか？という問いに答える前に、
以下のプログラムを実行してみて下さい。
function ffttest
%
% 高速フーリエ変換テスト
% ３Ｈｚ、３．１ＨｚのＳＩＮ波をフーリエ変換する
% 窓関数は方形波を使用
%
%
fs=256; % サンプリング周波数
fftpt=fs*16; % フーリエ変換の精度
f1=3; % 青線波形の周波数
f2=3.1; % 緑線波形の周波数
t=(0:1/fs:1-1/fs); % ｘ軸のデータ長
x1=sin(2*pi*f1*t); % 青線サイン波の生成
x2=sin(2*pi*f2*t); % 緑線サイン波の生成
subplot(2,1,1);
plot(t,x1,'b');
hold on;
plot(t,x2,'g');
xlabel('time');
y1=fft(x1,fftpt); % 青線サイン波のフーリエ変換
y2=fft(x2,fftpt); % 緑線サイン波のフーリエ変換
fq=((0:fftpt-1)/fftpt)*fs; % 周波数ｘ軸のデータ長
subplot(2,1,2);
plot(fq,20*log10(abs(y1)),'b'); % 縦軸をｄＢ表示
hold on;
plot(fq,20*log10(abs(y2)),'g'); % 縦軸をｄＢ表示
axis([0 30 -50 50]);
xlabel('frequency');
ylabel('amplitude(dB)');
|
function ffttest
%
% 高速フーリエ変換テスト
% ３Ｈｚ、３．１ＨｚのＳＩＮ波をフーリエ変換する
% 窓関数は方形波を使用
%
%
fs=256; % サンプリング周波数
fftpt=fs*16; % フーリエ変換の精度
f1=3; % 青線波形の周波数
f2=3.1; % 緑線波形の周波数
t=(0:1/fs:1-1/fs); % ｘ軸のデータ長
x1=sin(2*pi*f1*t); % 青線サイン波の生成
x2=sin(2*pi*f2*t); % 緑線サイン波の生成
w=hanning(fs); % 窓かけ準備
w=w'; % ハニングは列データなので、行データへ転置
x1=x1.*w; % 窓かけ操作
x2=x2.*w;
subplot(2,1,1);
plot(t,x1,'b');
hold on;
plot(t,x2,'g');
xlabel('time');
y1=fft(x1,fftpt); % 青線サイン波のフーリエ変換
y2=fft(x2,fftpt); % 緑線サイン波のフーリエ変換
fq=((0:fftpt-1)/fftpt)*fs; % 周波数ｘ軸のデータ長
subplot(2,1,2);
plot(fq,20*log10(abs(y1)),'b'); % 縦軸をｄＢ表示
hold on;
plot(fq,20*log10(abs(y2)),'g'); % 縦軸をｄＢ表示
axis([0 30 -50 50]);
xlabel('frequency');
ylabel('amplitude(dB)');
|
